Ni havas la jenan triangulon kun punkto \(p\).
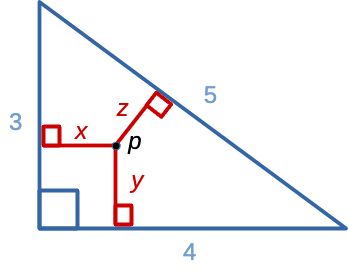
La tasko estas solvi \(x, y\) kaj \(z\) tiel, ke \(x^2+y^2+z^2\) havas sian minimuman valoron. Alivorte temas pri trovi la punkton de Fermat1 aŭ geometrian meznombron en ĉi tiu triangulo.
Eblas solvi la problemon per trigonometrio (traktu la punkton \(p\) kiel originon kaj \(x^2+y^2+z^2\) kiel ebenon) aŭ per krei ekvacion kaj kalkuli ĉi ties trian derivaĵon, sed tiuj povas esti tro malfacilaj metodoj.
Anstataŭe ni utiligu la malegalecon de Cauchy–Schwarz [fi], ankaŭ konata kiel la malegaleco de Cauchy–Bunjakovski–Schwarz2. Ĉar ni havas tri variablojn, ni uzu la sekvan version de la malegaleco:
$$
(a^2+b^2+c^2)(d^2+e^2+f^2) \ge (ad+be+cf)^2 \tag{1}
$$
La \(a,b\) kaj \(c\) klare respondas al \(x,y\) kaj \(z\) en nia problemo, do ni bezonas trovi taŭgajn \(d,e\) kaj \(f\). Por tiu celo ni devas iel ligi \(x,y\) kaj \(z\) al la nombroj 3, 4 kaj 5.
Ni desegnu tri aldonajn triangulojn enen de la triangulo:
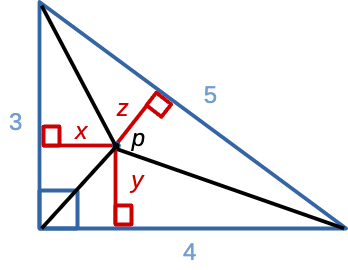
Per tiuj tri aldonaj trianguloj ni povas esprimi la areon de la origina triangulo:
$$
A=\frac{1}{2} (4 \cdot 3) = \frac{1}{2} (3 \cdot x) + \frac{1}{2} (4 \cdot y) + \frac{1}{2} (5 \cdot z)
$$
Baze sur tio ni povas krei la jenan egalecon:
$$
3x+4y+5z=12 \tag{2}
$$
Tiu egaleco funkcias kiel limigo por la solvo, kaj fakte eblas solvi la problemon per optimumado3. Tamen pli simple estas per la malegaleco de Cauchy–Schwarz \((1)\), kiun ni nun povas esprimi jene dank’ al \((2)\):
$$
\begin{align*}
(x^2+y^2+z^2)(3^2+4^2+5^2) &\ge (3x+4y+5z)^2
\\ (x^2+y^2+z^2) \cdot 50 &\ge 12^2
\\ x^2+y^2+z^2 &\ge \frac{144}{50}
\\ x^2+y^2+z^2 &\ge \frac{72}{25}
\end{align*} \tag{3}
$$
Notu, ke la egaleco en la malegaleco de Cauchy–Schwarz \((1)\) validas nur kaj nur tiam, kiam4
$$\frac{a}{d} = \frac{b}{e} = \frac{c}{f}$$
Uzante tion ni ricevas el la unua linio de \((3)\):
$$
\begin{align*}
\frac{x}{3} &= \frac{4}{y} = \frac{5}{z}
\\y&=\frac{4}{3}x, z=\frac{5}{3}x
\end{align*} \tag{4}
$$
Tiujn ni povas enmeti en \((2)\) kaj ricevi post elementaj aritmetikaj operacioj:
$$
\begin{align*}
3x+4(\frac{4}{3}x)+5(\frac{5}{3}x) &=12
\\x &= \frac{18}{25}
\end{align*}
$$
Estas simple kalkuli la valorojn de \(y\) kaj \(z\) uzante la rezultojn el \((4)\):
$$
\begin{align*}
y &= \frac{4}{3} x= \frac{4}{3} \cdot \frac{18}{25} = \frac{24}{25}
\\z &= \frac{5}{3} x = \frac{5}{3} \cdot \frac{18}{25} = \frac{6}{5}
\end{align*}
$$
Do la solvo estas5
$$x = \frac{18}{25}, y = \frac{24}{25}, z = \frac{6}{5}$$
Fonto: mallonga filmo [en]en Jutubo en la kanalo blackpenredpen
- La punkto nomiĝas la punkto de Fermat aŭ la punkto de Fermat kaj Torricelli honore al la franca matematikisto Pierre de Fermat, kiu prezentis la problemon kaj la itala matematikisto Evangelista Torricelli, kiu solvis la problemon. ↩︎
- Laŭ Augustin Louis Cauchy, Viktor Bunjakovski [en] kaj Hermann Schwarz [en], kiuj pruvis la malegalecon en diversaj kuntekstoj. ↩︎
- Ekzemple per la multiplikantoj de Lagrange [en]. ↩︎
- Se vi interpretas la termojn en la malegaleco de Cauchy-Schwarz kiel vektorojn, la egaleco validas nur tiam, kiam la vektoroj estas lineare sendependaj. ↩︎
- Estas ĉiam bona ideo kontroli la rezulton. Do $$\left(\frac{18}{25}\right)^2 + \left(\frac{24}{25}\right)^2 + \left(\frac{6}{5}\right)^2 = \frac{1800}{25^2}= \frac{72}{25}$$ ↩︎