Vi havas poŝlampon kaj ok bateriojn1, el kiuj duono havas ŝargon kaj duono estas tute senŝargaj. La poŝlampo enspacas du bateriojn, kaj ambaŭ devas havi ŝargon, por ke la lampo lumu – unu baterio kun ŝargo ne sufiĉas. Ekstere ĉiuj baterioj aperas similaj, do vi ne povas diri, ĉu baterio havas ŝargon aŭ ne sen testi ĝin. Unu testo konsistas, ke vi metas du bateriojn en la lampon kaj prenas la butonon por ekscii, ĉu la lampo eklumas.



Tasko
Se vi hazarde prenas du bateriojn, en la plej bona okazo vi elektas du bateriojn kun ŝargo, kaj la lampo eklumas, kiam vi testas. Sed ni pritraktu la plej malbonan okazon, kiam vi devas fari la maksimuman nombron da testoj, antaŭ ol vi povas esti certa, ke la lampo enhavas du bateriojn kun ŝargo. Kiom da testoj estas la minimuma nombro, por ke vi povas esti certa en la plej malbona okazo? Enkalkulu la finan teston, en kiu la lampo eklumas.
Brutforta metodo
Antaŭ ol provi trovi la minimuman nombron ni trovu eĉ unu metodon, per kiu ni povas esti certaj, ke la lampo enhavas du bateriojn kun ŝargo. Ni komencu per la evidenta metodo, kiu bazas sur forto.
Ni numeru la bateriojn de 1 ĝis 8. Ni testu la baterion 1 kun ĉiu alia. En la plej malbona okazo neniu el la paroj (1,2), (1,3), (1,4), (1,5), (1,6), (1,7) kaj (1,8) sukcesigas la lampon eklumi. Ni povas konkludi, ke la baterio 1 estas senŝarga.








Ni ripetu kun la baterio 2. En la plej malbona okazo neniu el la paroj (2,3), (2,4), (2,5), (2,6), (2,7) kaj (2,8) sukcesigas la lampon eklumi.








Ni povas konkludi, ke la baterio 2 estas senŝarga. Ni simile ripetu kun la baterioj 3 kaj 4.
Post ĉi tiuj testoj ni povas konstati, ke ni trovis ĉiujn kvar senŝargajn bateriojn kaj la kvar restaj devas havi ŝargon.








Ni arbitre elektas du el la kvar restaj kaj faras la finan teston, en kiu la lampo eklumas. Entute ni faras jenajn testojn:
| testoj | konkludo |
|---|---|
| (1,2), (1,3), (1,4), (1,5), (1,6), (1,7), (1,8) | la baterio 1 estas senŝarga |
| (2,3), (2,4), (2,5), (2,6), (2,7), (2,8) | la baterio 2 estas senŝarga |
| (3,4), (3,5), (3,6), (3,7), (3,8) | la baterio 3 estas senŝarga |
| (4,5), (4,6), (4,7), (4,8) | la baterio 4 estas senŝarga |
| (5,6) | la fina testo |
Do en la plej malbona okazo per ĉi tiu brutforta metodo ni faras 7 + 6 + 5 + 4 + 1 = 23 testojn.
Sed certe estas pli bonaj metodoj, pli bonaj en la senco, ke ni bezonas fari malpli da testoj por esti certaj.
Metodo kun paroj
Ĉi-foje ni testu la bateriojn laŭpare (1,2), (3,4), (5,6) kaj (7,8). En la plej malbona okazo neniu paro sukcesigas la lampon eklumi. Ni povas konkludi, ke ĉiu paro devas havi minimume unu senŝargan baterion. Ĉar estas entute kvar senŝargaj baterioj, ni povas konstati, ke ĉiu paro havas ekzakte unu senŝargan baterion. La alia baterio en ĉiu paro devas havi ŝargon.








Ni elektu du parojn, {1,2} kaj {3,4}, kaj sisteme testu tiujn bateriojn: (1,3), (1,4), (2,3) kaj (2,4). En la plej malbona okazo nur la plej lasta paro sukcesigas la lampon eklumi.
| testoj | konkludo |
|---|---|
| (1,2), (3,4), (5,6), (7,8) | ĉiu paro konsistas el kunŝarga kaj senŝarga baterio |
| (1,3), (1,4), (2,3), (2,4) |
Do en la plej malbona okazo per ĉi tiu metodo ni faras 4 + 4 = 8 testojn.
Tiu metodo kun paroj klare estas pli bona ol tiu unua, brutforta, metodo. Ĉu estas aliaj metodoj?
Metodo kun du grupoj
Ni grupigu la bateriojn en du grupojn: {1,2,3,4} kaj {5,6,7,8}. Ni testu la unuan grupon sisteme: (1,2), (1,3), (1,4), (2,3), (2,4) kaj (3,4). En la plej malbona okazo neniu paro sukcesigas la lampon lumiĝi. Ni povas konkludi, ke inter la kvar baterioj de la grupo devas esti minimume tri senŝargaj. Devas esti ĉi tiel, ĉar estus malpli ol tri baterioj kun ŝargo inter tiuj kvar, la lampo eklumus, kiam ni testas ĉiun paron.




Kion signifas tiu ”minimume tri senŝargaj”? Ni supozu, ke ĉiuj kvar estas senŝargaj. Ĉi tiam sufiĉas, ke ni arbitre elektas du bateriojn el la dua grupo (la grupo {5,6,7,8}), kiuj baterioj devas esti kunŝargaj, kaj faras la finan teston. Ĉi tiam ni faras 6 + 1 = 7 testojn.
Se estas nur tri senŝargaj en la unua grupo, ĉi tiam la dua grupo enhavas unu senŝargan kaj tri kunŝargaj. Sufiĉas, ke ni testas du parojn: (5,6) kaj (7,8). Ĉi tiam ni faras 6 + 2 = 8 testojn.
| testoj | konkludo |
|---|---|
| (1,2), (1,3), (1,4), (2,3), (2,4), (3,4) | inter ĉi tiuj kvar baterioj estas minimume tri senŝargaj |
| (5,6), (7,8) |
Do en la plej malbona okazo per ĉi tiu dugrupa metodo ni faras 6 + 2 = 8 testojn.
Ni trovis du metodojn, per kiuj sufiĉas ok testoj. Ĉu ok testoj estas la minimuma nombro de testoj, kiun oni bezonas por esti certa en la plej malbona okazo?
Metodo kun tri grupoj
Ĉi-foje ni grupigu la bateriojn en tri grupojn: {1,2,3}, {4,5,6} kaj {7,8}. Ni testu ambaŭ grupoj kun tri baterioj sisteme: (1,2), (1,3,) kaj (2,3) resp. (4,5), (4,6) kaj (5,6). Se la lampo ne eklumas ĉe ambaŭ grupo, la grupoj devas enhavi minimume po du senŝargajn bateriojn. Devas esti ĉi tiel, ĉar estus nur unu senŝarga baterio en unu aŭ alia grupo, la lampo eklumus dum testado de tiu grupo.








Sed estas entute nur kvar senŝargaj baterioj, ni povas konstati, ke la grupo de du baterioj havas nur baterioj kun ŝargo. Ni faras la finan teston (7,8), kaj la lampo eklumas.
| testoj | konkludo |
|---|---|
| (1,2), (1,3,), (2,3) | inter tiuj tri baterioj estas minimume du senŝargaj |
| (4,5), (4,6), (5,6) | inter tiuj tri baterioj estas minimume du senŝargaj |
| (7,8) | la fina testo |
Do en la plej malbona okazo per ĉi tiu trigrupa metodo ni faras 3 + 3 + 1 = 7 testojn.
Ĉu sep testoj estas la minimumo?
Ĉu sep testoj estas la minimuma nombro de testoj, kiun oni bezonas por esti certa en la plej malbona okazo? Ni asertas, ke jes. Por pruvi ĉi tion ni devas montri, ke ses testoj ne sufiĉas por trovi du bateriojn kun ŝargo. Por montri tion ni apogas sur la grafeoteorion. La baterioj estu verticoj aŭ punktoj kaj eĝo aŭ latero inter du punktoj reprezentu teston kun tiuj du baterioj. La tasko montri, ke ses testoj ne sufiĉas por trovi du bateriojn kun ŝargo, grafeoteorie egalas, ke ni montru, ke en grafeo kun ok punktoj kaj nur ses lateroj eblas ekzisti kvar aŭ pli da punktoj sen lateroj inter ili. Alivorte kvar punktoj – la kunŝargaj baterioj – povas ”kaŝi sin” en tia grafeo.
Ni pruvas ĉi tion per kontraŭekzemplo. Ni supozu, ke en grafeo kun ok punktoj povas ekzisti maksimume tri reciproke seninterligitaj punktoj, kiam la grafeo havas ses laterojn. Lasu tiuj tri punktoj esti {1,2,3}. Ni grupigu la bateriojn en du grupojn: tiun kun la tri punktoj {1,2,3} kaj la reston {4,5,6,7,8}. Ni pritraktu arbitran baterion el la dua grupo, lasu tiun esti la baterio 4. Ni supozu, ke ne ekzistas latero inter ĉi tiu kaj la baterioj en la unua grupo. Sed ĉi tiam la baterioj {1,2,3,4} formas aron de kvar seninterligitaj punktoj kontraŭe al nia supozo.
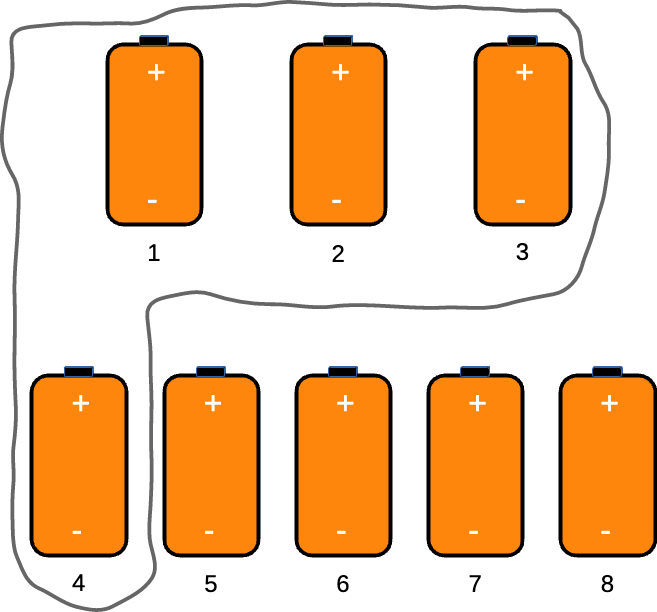
Ni konstatas, ke la baterio 4 devas ligi al unu baterio el la unua grupo.
Simile ĉiuj aliaj baterioj en la dua grupo devas ligi al unu baterio el la unua grupo. Tio signifas, ke la grafeo nun havas kvin laterojn.
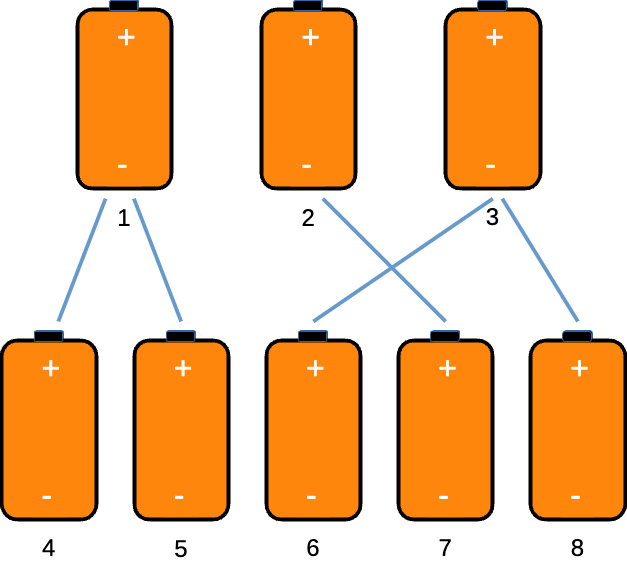
Inter kiujn punktojn ni povas meti la lastan, sesan lateron? Ni denove elektu la baterion 4 kaj ligu ĝin al unu baterio el la unua grupo {1,2,3}. Ĉar ni supre ligis la baterion 4 al la baterio 1, ni ĉi-foje ligu ĝin al la baterio 2. Ĉi tiam la baterioj {4,5,6,7,8} formas aron de kvin seninterligitaj punktoj. Se ni anstataŭe ligas la baterion 4 al unu el la dua grupo {4,5,6,7,8}, ni diru 52, ĉi tiam la baterioj {5,6,7,8} formas aron de kvar seninterligitaj punktoj.
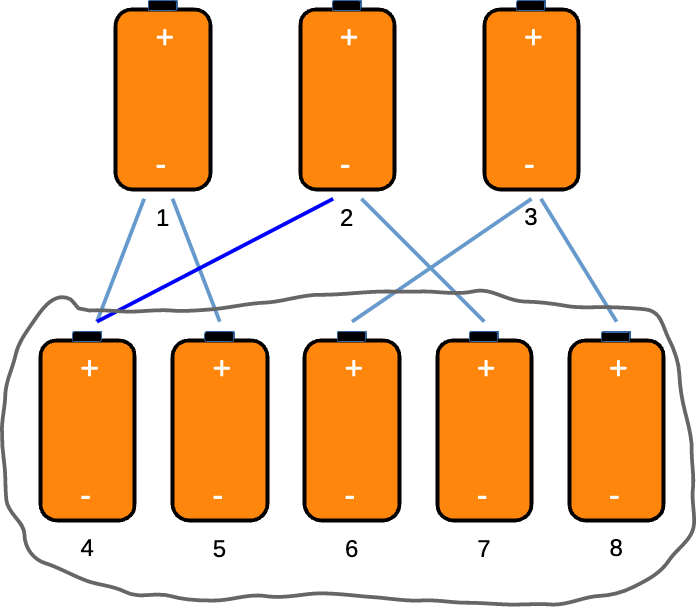
Ĉar la grupigo en du grupojn (jen {1,2,3} kaj {4,5,6,7,8}) estas tute arbitra, ni povas konstati, ke ses lateroj ne sufiĉas kovri la ok punktoj tiel, ke ne ekestas aro de (minimume) kvar seninterligitaj punktoj. Alivorte la kvar baterioj kun ŝargo povas ”kaŝi sin” inter tiuj kvar seninterligitaj, sentestitaj, punktoj.
Ĉar ni antaŭe montris, ke ekzistas metodo, per kiu sep testoj sufiĉas eĉ en la plej malbona okazo, ni konstatu, ke ni trovis la plej efikan metodon trovi du bateriojn kun ŝargaĵo inter ok baterioj.
Fontoj:
- Jutuba filmo [en] en la kanalo MindYourDecisions
- grafeoteoria artikolo [en] de Bogumił Kamiński
- Kiam mi komencis verki ĉi tiun artikolon, mi trovis artikolojn pri baterioj kaj piloj en Vikipedio, kaj mi konfuziĝis. Montriĝis, ke la artikolo pri pilo estas iomete devojiga. Pilo havas tension de 1,5 V kaj estas tiu, kiun on en kelkaj lingvoj nomas elektra paro, ekz. [fi] sähköpari. Unu baterio kutime enhavas multajn pilojn, kiuj povas esti paralele aŭ serie koneksaj. ↩︎
- Tiu devas esti alia ol la baterio 4, ĉar vi ne povas testi baterion kun si mem. ↩︎